ФИПИ Задание 4777, 4796

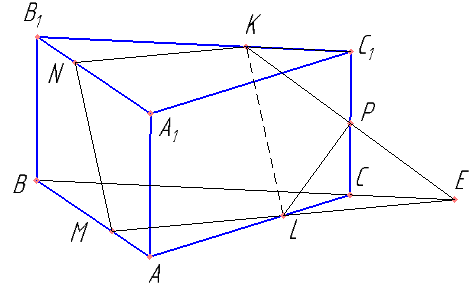
В правильной треугольной призме $A B C A_{1} B_{1} C_{1}$ сторона основания $A B$ равна 6, а боковое ребро $A A_{1}$ равно $ 2\sqrt{2} $. На рёбрах $A B$ , $A_{1} B_{1}$ и $B_{1} C_{1}$ отмечены точки $M$ , $N$ и $K$ соответственно, причём $A M = B_{1} N = C_{1} K = 2$ .

а) Пусть $L$ $—$ точка пересечения плоскости $M N K$ с ребром $A C$ . Докажите, что $M N K L$ $—$ квадрат.

б) Найдите площадь сечения призмы плоскостью $M N K$ .

В правильной треугольной призме $A B C A_{1} B_{1} C_{1}$ сторона основания $A B$ равна 3, а боковое ребро $A A_{1}$ равно $ \sqrt{2} $. На рёбрах $A B$ , $A_{1} B_{1}$ и $B_{1} C_{1}$ отмечены точки $M$ , $N$ и $K$ соответственно, причём $A M = B_{1} N = C_{1} K = 1$ .

а) Пусть $L$ $—$ точка пересечения плоскости $M N K$ с ребром $A C$ . Докажите, что $M N K L$ $—$ квадрат.

б) Найдите площадь сечения призмы плоскостью $M N K$ .

$В правильной треугольной призме ABCA1B1C1 сторона основания AB равна 6, а боковое ребро AA1 равно $ 2\sqrt{2} $. На рёбрах AB, A1B1 и B1C1 отмечены точки M, N и K соответственно, причём AM=B1N=C1K=2. а) Пусть L — точка пересечения плоскости MNK с ребром AC. Докажите, что MNKL — квадрат. б) Найдите площадь сечения призмы плоскостью MNK.$

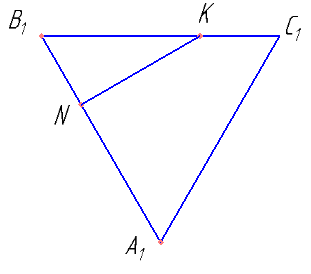
Если не полениться и построить дополнительный чертеж верхнего основания призмы, то похоже, что NK перпендикулярно A $A M = B_{1} N = C_{1} K = 2$ B $A M = B_{1} N = C_{1} K = 2$ .

Найти NK. доказать, что треугольник B $A M = B_{1} N = C_{1} K = 2$ NK — прямоугольный.

По определению угла между прямой и плоскостью — NK перпендикулярна плоскости ABB $A M = B_{1} N = C_{1} K = 2$ A $A M = B_{1} N = C_{1} K = 2$ . Т.к. LM параллельна NK, то она тоже перпендикулярна ABB $A M = B_{1} N = C_{1} K = 2$ A $A M = B_{1} N = C_{1} K = 2$ . Найти ML. Обоснуйте, что $M N K L$ $—$ квадрат.

Найти BE, CE. Доказать, что P — середина отрезка CC $A M = B_{1} N = C_{1} K = 2$ . Найти KP, LP. Доказать, что треугольник KPL — прямоугольный.

Ответ: 15; 3, 75.