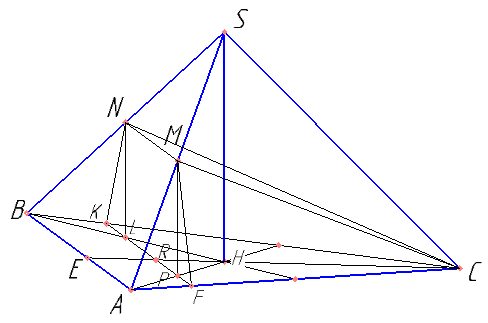
В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 8. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.
В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 7. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5:1, считая от точки C.
б) Найдите объём пирамиды, вершиной которой является точка C, а основанием — сечение пирамиды SABC плоскостью α.
Доказать,что LP — средняя линия треугольника BHA.
Найти EH:HC, ER:RH, ER:RC.
Найти EC, RC, KF, NM, SH, MP.
Ответ: \( \frac{80\sqrt{3}}{3} \), \( \frac{20\sqrt{3}}{3} \),