В треугольной пирамиде MABC основанием является правильный треугольник ABC, ребро MB перпендикулярно плоскости основания, стороны основания равны 3, а ребро MA равно 5. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM- точка L. Известно, что AD=AL=2 и BE=1. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
В треугольной пирамиде MABC основанием является правильный треугольник ABC, ребро MB перпендикулярно плоскости основания, стороны основания равны 3, а ребро MA равно \( \sqrt{13} \). На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM- точка L — середина ребра. Известно, что AD=2 и BE=1. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
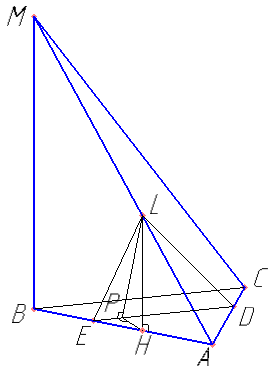
LH перпендикулярно BA. Обосновать, что LH перпендикулярно плоскости основания. Обосновать, что LPH — искомый угол.
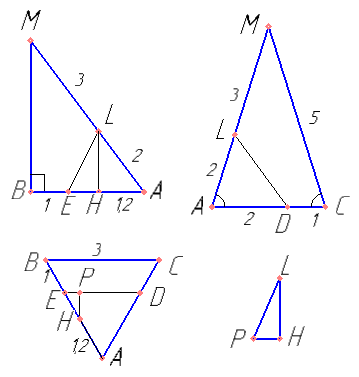
Сделать дополнительные чертежи треугольников BMA, AMC, ABC, LPH. Не ленитесь делать дополнительные чертежи — ошибок будет меньше.
Найти длины всех отрезков с учетом дополнительных построений. Найти LH и PH.
Ответ: \( arctg(\frac{4\sqrt{3}}{3}) \), \( arctg(\frac{4\sqrt{3}}{3}) \)
