В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые рёбра равны 5. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что AD=AE=AL=4. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM — точка L. Известно, что CD=BE=AL=2. Найдите угол между плоскостью основания и плоскостью, проходящей через точки E, D и L.
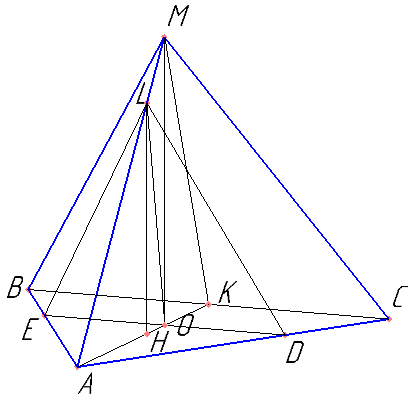
Определить тип треугольника AED. Пусть O — середина ED. Доказать, что точка O — основание высоты пирамиды. Найти AO. Найти MO.
Найти LH — высоту треугольника ALO. Найти HO.
Обосновать, что LO перпендикулярно ED, а угол LOH — искомый.
Ответ: \( arctg(2\sqrt{\frac{13}{3}}) \), \( arctg(\frac{\sqrt{39}}{9}) \)
