В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые рёбра равны 10. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM- точка L. Известно, что AD=AE=LM=4. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
В правильной треугольной пирамиде MABC с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре AC находится точка D, на ребре AB находится точка E, а на ребре AM- точка L. Известно, что CD=BE=LA=2. Найдите площадь сечения пирамиды плоскостью, проходящей через точки E, D и L.
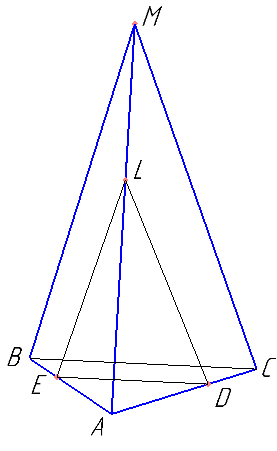
Определить тип треугольника AED. Найти ED.
Определить тип треугольника ELD. Найти AL.
Чему равен \( cos(\angle BAM) \). Найти EL.
В равнобедренном треугольнике основание равно 4, а боковые стороны \( \sqrt{14} \). Найти высоту проведенную к основанию.
Ответ: \( 8\sqrt{2,1} \), \( 2\sqrt{10} \)
