В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=4, AD=3, AA1=7. Точка O принадлежит ребру BB1 и делит его в отношении 3:4, считая от вершины B. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки A, O и C1.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=5, AD=3, AA1=8. Точка R принадлежит ребру AA1 и делит его в отношении 3:5, считая от вершины A. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки B, R и D1.
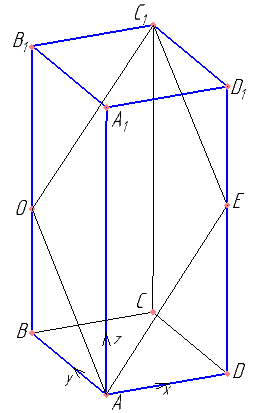
Найти AO и AE. Определить тип четырехугольника AOC1E.
Найти координаты векторов \( \overrightarrow{AO} \) и \( \overrightarrow{AE} \), \( cos(\angle{OAE}) \).
Найти \( sinA \), если \( cosA=\frac{12}{25} \).
Ответ:\( \sqrt{481} \), \( \sqrt{931} \).
