В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку C и середину ребра MA параллельно прямой BD.
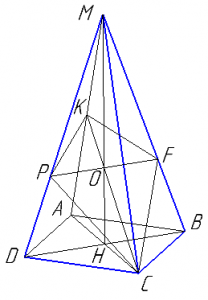
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 4, а боковые рёбра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Обосновать, что KC перпендикулярно PF.
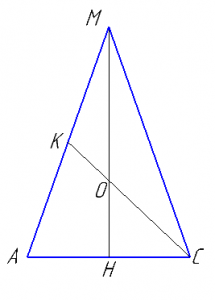
В равнобедренном треугольнике с основанием \( 6\sqrt{2} \) и боковыми сторонами 12 найти медиану проведенную к боковой стороне.
В каком отношении делит медианы точка их пересечения? Найти PF.
Вспомнить формулу расчета площади любого выпуклого четырехугольника через диагонали.
Ответ: 24,, \( \frac{32}{3} \).
