Задание 2020/3

Дан прямоугольный треугольник ABC. На катете AC отмечена точка M, а на продолжении катета BC за точку C — точка N так, что CM = CB и CA = CN.

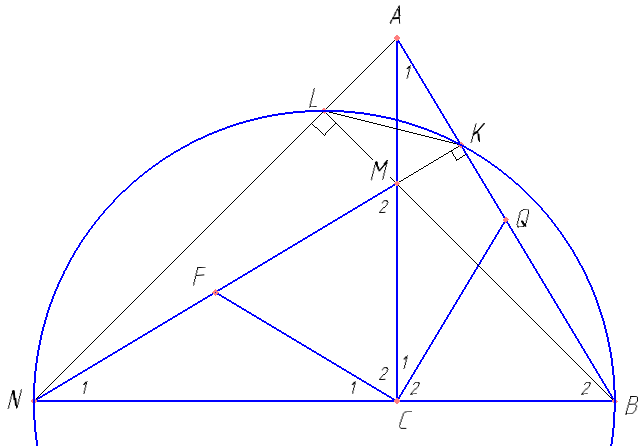
а) Пусть CQ и CF — медианы треугольников ABC и NMC соответственно. Докажите, что CF и CQ перпендикулярны.

б) Пусть L — это точка пересечения BM и AN, K — точка пересечения NM и AB, BC = 3, AC = 5. Найдите KL.

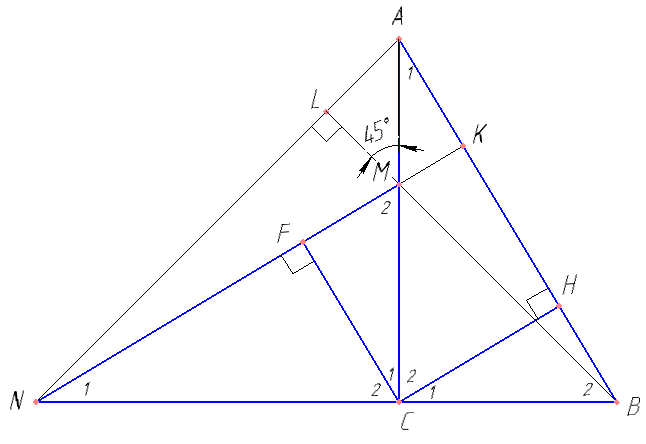
а) Отрезки CH и CF — высоты треугольников ACB и NCM соответственно. Докажите, что CF и CH перпендикулярны.

б) Прямые BM и AN пересекаются в точке L. Найдите LM, если  BC = 4, а AC = 8.

Дан прямоугольный треугольник ABC. На катете AC отмечена точка M, а на продолжении катета BC за точку C — точка N так, что CM = CB и CA = CN. а) Пусть CQ и CF — медианы треугольников ABC и NMC соответственно. Докажите, что CF и CQ перпендикулярны. б) Пусть L — это точка пересечения BM и AN, K — точка пересечения NM и AB, BC = 3, AC = 5. Найдите KL.Дан прямоугольный треугольник ABC. На катете AC отмечена точка M, а на продолжении катета BC за точку C — точка N так, что CM = CB и CA = CN. а) Пусть CQ и CF — медианы треугольников ABC и NMC соответственно. Докажите, что CF и CQ перпендикулярны. б) Пусть L — это точка пересечения BM и AN, K — точка пересечения NM и AB, BC = 3, AC = 5. Найдите KL.

Найти равные углы в прямоугольном треугольнике с медианой построенной из прямого угла.

Найти равные углы в прямоугольном треугольнике с высотой построенной из прямого угла.

Рассчитать углы NLB, NKB, LMA.

Какому треугольнику подобен треугольник ALK,  а какому AMK? Найти AK, LK.

В равнобедренном прямоугольном треугольнике с гипотенузой 4 найти катеты. Найти  AM, LM.

Ответ:  ​\( \frac{8}{\sqrt{17}} \)​,  ​\( 2\sqrt{2} \)​.