На сторонах BC, AC и AB треугольника ABC отмечены точки A1, B1 и C1 соответственно, причем BA1:A1C=1:2. AB1:B1C=1:3. AC1:C1B=8:3. Отрезки BB1 и CC1 пересекаются в точке D.
а) Докажите, что ADA1B1 — параллелограмм.
б) Найдите радиус описанной около треугольника ABC окружности, если AD перпендикулярно BC, AC=16, BC=15.
б) Найдите CD, если AD перпендикулярно BC, AC=28, BC=18.
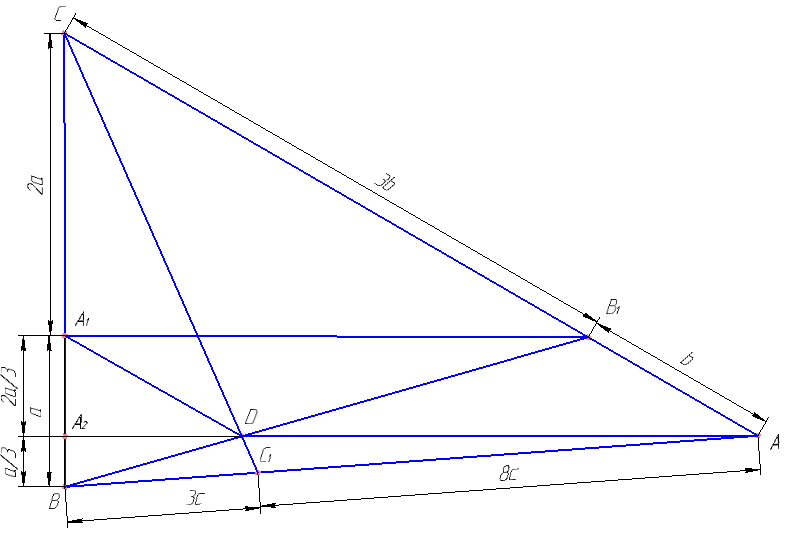
Выразить BA2 и A2A1 через a, используя теорему Чевы.
Найти отношение BD к DB1, используя теорему Менелая.
В треугольнике ABC AB=\( \sqrt{18} \), AC=6. На стороне AB взяли точку M, а на стороне AC точку N. AM=\( \sqrt{2} \). AN=1. Доказать, что треугольник ABC подобен треугольнику AMN.
Доказать подобие треугольников CA2A и CA1B1. Доказать подобие треугольников BB1C и BDA1.
Найти \( cosC \). Найти AB используя теорему косинусов.
Вспомнить формулы площадей треугольника. Найти площадь треугольника ABC. Найти радиус описанной окружности.
Чему равно A1D? Найти используя доказательство первого пункта. Найти A2A1 , A2D, CD.
Ответ: \( \frac{27}{\sqrt{11}} \), 17.
