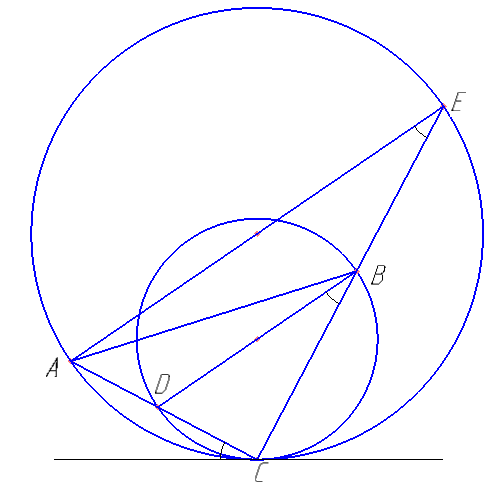
Две окружности касаются внутренним образом в точке C. Вершины A и B равнобедренного прямоугольного треугольника ABC c прямым углом C лежат на большей и меньшей окружностях соответственно. Прямая AC вторично пересекает меньшую окружность в точке D. Прямая BC вторично пересекает большую окружность в точке E.
а) Докажите, что AE параллельно BD.
б) Найдите AC, если радиусы окружностей равны 8 и 15.
Угол между хордой и касательной.
Прямоугольный треугольник с катетами 9 и 12 вписан в окружность. Найти радиус этой окружности.
Пусть AC=x. Выразить DC через x, используя условие задачи.
В равнобедренном прямоугольном треугольнике ABC с прямым углом C катет AC разбит точкой M так, что AM:MC=7:8. MB=16. Найти AC.
Ответ: \( \frac{240}{17} \).
