Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает продолжение стороны CD за точку D в точке K.
а) Докажите, что AE=AK.
б) Найдите отношение KE:BD, если ∠BAD=60°
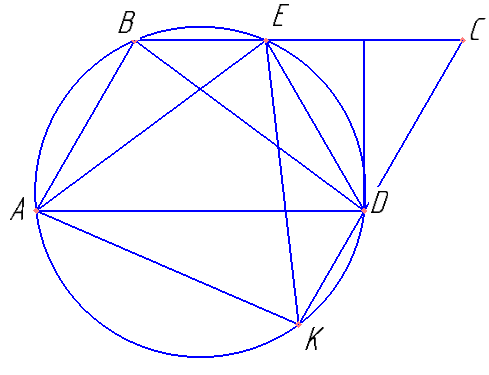
Доказать, что ABED — равнобедренная трапеция.
Доказать, что угол ADE равен углу DCE и равен углу ADK.
Найти углы ADE, DCE, ADK, EDK, EAK.
В окружность вписаны два треугольника ABD и EAK. Угол BAD = 60° , и угол EAK= 60°.. Найти отношение \( \frac{KE}{BD} \).
Ответ: 1.
