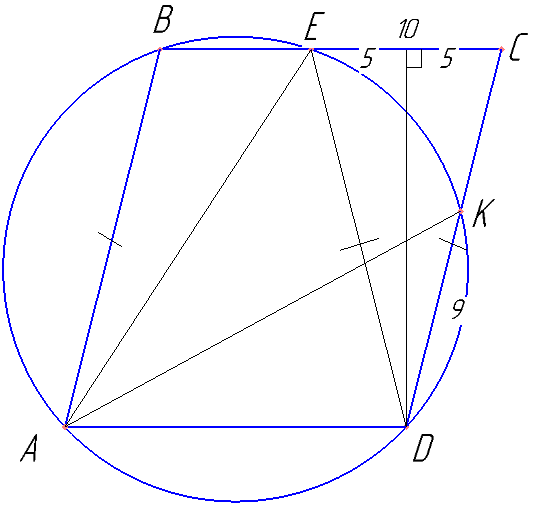
Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и E и пересекает сторону CD в точках K и D.
а) Докажите, что AE=AK.
б) Найдите AD, если CE=10, DK=9 и cos∠BAD=0,2
Доказать, что в окружности равные вписанные углы опираются на равные хорды. Что доказывает пункт а).
Доказать, что трапеция вписанная в окружность равнобедренная.
Основание равнобедренного треугольника равно 10, а косинус угла при основании 0,2. Найти боковую сторону. Найти CK.
DK=9, CD=25, EC=10. Найти BC. Используйте теорему о двух секущих.
Ответ: 40.
