Окружность с центром O1 касается оснований BC и AD и боковой стороны AB трапеции ABCD. Окружность с центром O2 касается сторон BC, CD и AD. Известно, что AB=10, BC=9, CD=30, AD=39.
а) Докажите, что прямая O1O2 параллельна основаниям трапеции ABCD.
б) Найдите O1O2.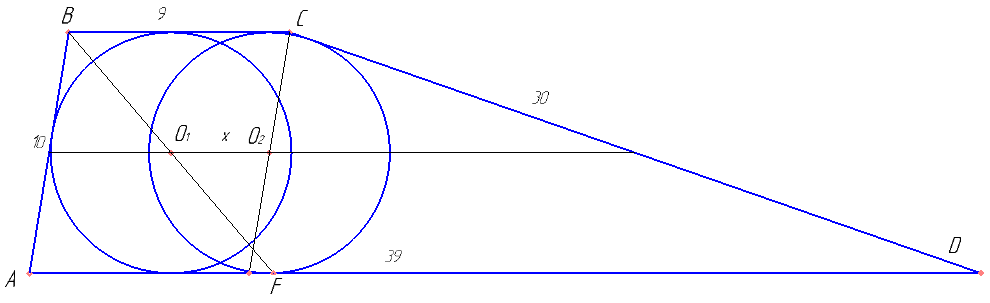
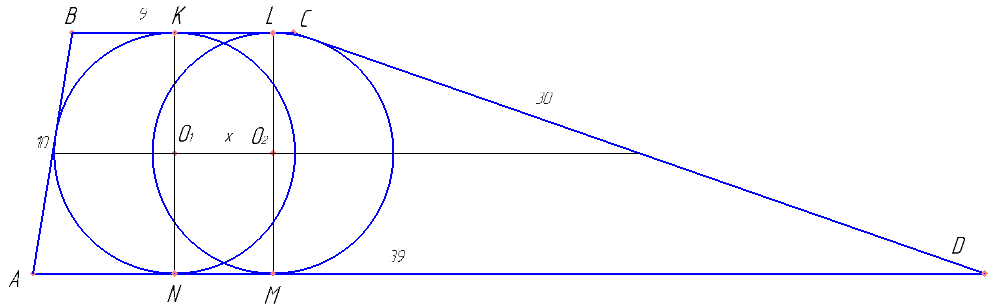
Доказать, что высоты трапеции проведенные через центра окружностей проходят через точки касания окружностей. Доказать, что KLO2O1 — параллелограмм.
Окружность внутренним образом касается оснований AD и BC трапеции и боковой стороны AB. O-центр окружности. Отрезок BO продлили до пересечения со стороной AD в точке F.
— Доказать,что треугольник ABF равнобедренный.
— AB=10. Точка M – середина AB. Найти MO.
Второе решение — вырезать прямоугольник между центрами окружностей и соединить — получится описанный четырехугольник. Обозначить искомое расстояние за x. По теореме об описанном четырехугольнике можно найти x.
\[ 10+30=(39-x)+(9-x) \]
Oтвет: 4.
