Точка E—середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезки CK и BE пересекаются в точке O.
а) Докажите, что CO=KO.
б) Найдите отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 9:100 площади трапеции ABCD.
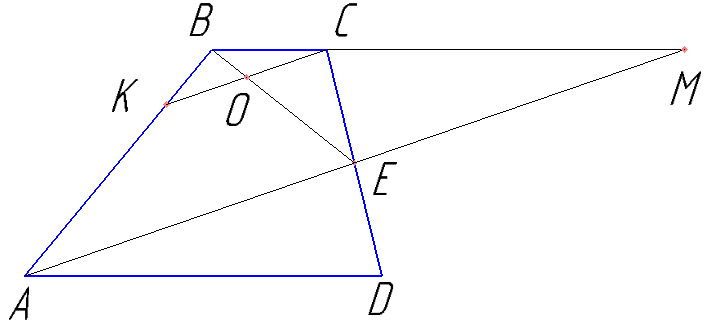
Обоснуйте подобие треугольников BKO и BAE; BCO и BME. Из двух тождеств пропорциональности отрезков следует доказательство пункта а).
Обоснуйте равенство площадей трапеции ABCD и треугольника ABM.
Площади подобных треугольников ABC и А1В1С1 относятся как 4:9. Найти коэффициент подобия треугольников.
В треугольнике АВM взяли точки К и C на сторонах АВ и ВM, так, что КC параллелен АM. Коэффициент подобия треугольников КВC и АВM равен 0,3. Найти отношение ВC:CM.
Ответ \( \frac{3}{7} \):
