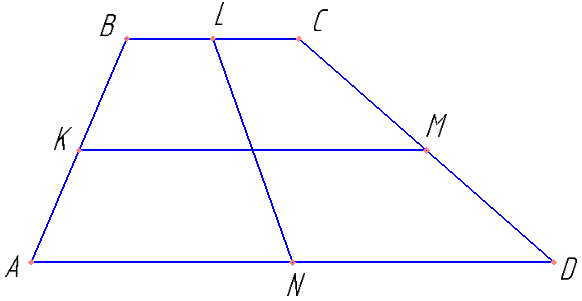
В выпуклом четырёхугольнике ABCD точки K, L, M и N — середины сторон AB, BC, CD и AD соответственно.
Площади четырёхугольников ABLN и NLCD равны, а площади четырёхугольников KBCM и AKMD относятся как 11:17.
а) Докажите, что прямые BC и AD параллельны.
б) Найдите отношение BC к AD.
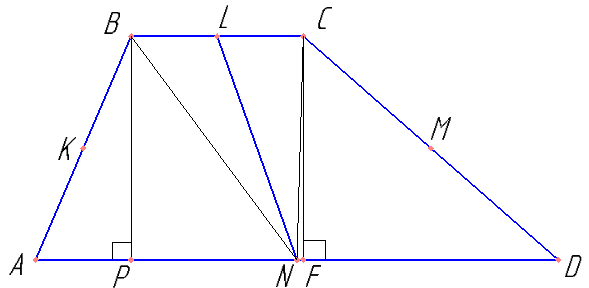
Доказать, что площадь треугольника BLN равна площади треугольника LCN.
Доказать, что площадь треугольника ABN равна площади треугольника NCD. Доказать, что их высоты равны и, что PBCF — параллелограмм. Отсюда следует доказательство пункта а).
Решение в общем виде с введением большого количества переменных. Обозначим AD через a, а BC через b. Высоту трапеции через h. Выразить отношение площадей трапеций KBCM и AKMD через переменные и приравнять к \( \frac{11}{17} \). Найти из тождества \( \frac{b}{a}. \)
Ответ: 0,4
