а) Докажите, что площади четырёхугольника AMOE и треугольника COD равны.
б) Найдите, какую часть от площади трапеции составляет площадь четырёхугольника AMOE, если BC=3, AD=4.
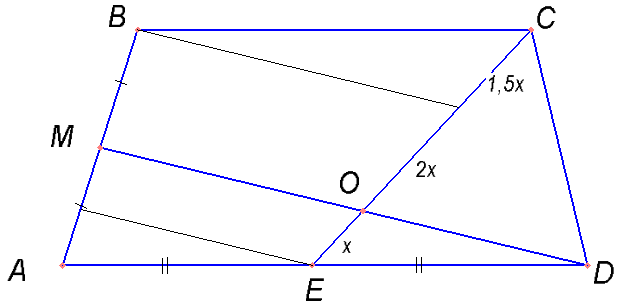
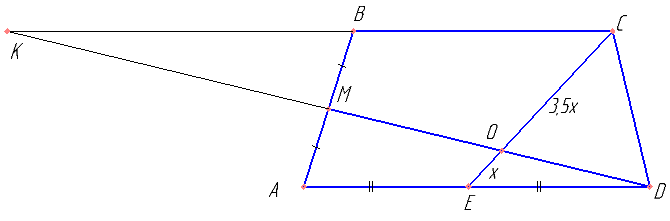
Дополнительные построения могут быть различными. Во втором чертеже — проще решение. В первом — красивее.
Доказать, что площади треугольников AMD и ECD равны. Вычитанием площади треугольника EOD доказывается пункт а).
Найти KB. Пусть EO — x. Выразить через x — OC.
Найти, какую часть от площади трапеции ABCD составляет площадь треугольника ECD.
На стороне AB треугольника ABC взяли точку M, так что AM:MC = 1:4. Найти — как относится площадь треугольника ABM к площади треугольника ABC.
Найти, какую часть от площади треугольника ECD составляет площадь треугольника EOD.
Ответ: \( \frac{2}{9} \).
