В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB=5, AC=8.
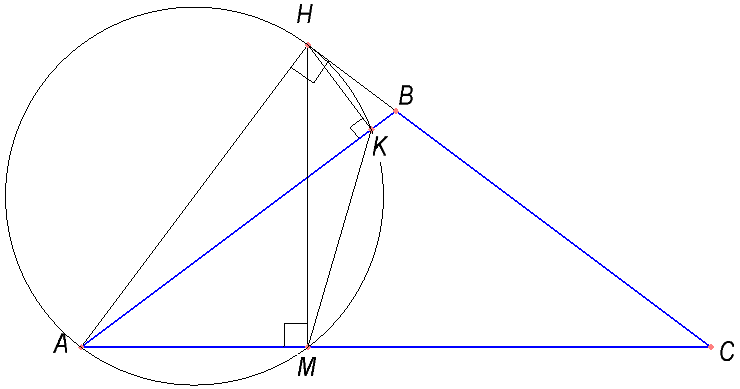
Удачное вспомогательное построение окружности. Вписанные углы, опирающиеся на одну и ту же дугу равны между собой. Найти равные углы в прямоугольном треугольнике с высотой построенной к гипотенузе.
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на основание AC опущен перпендикуляр HM. Доказать, что угол AHM равен углу ACB.
В четырехугольнике ABCD угол ACD и угол ABD прямые. Доказать, что угол BAC равен углу BDC.
Учитывая пункт а), надо найти AM.
Найти \( sin C \) в равнобедренном треугольнике ABC, с основание AC=8 и боковой стороной равной 5.
Доказать, что \( AM=AC*sin^2C \).
Ответ:2,88.