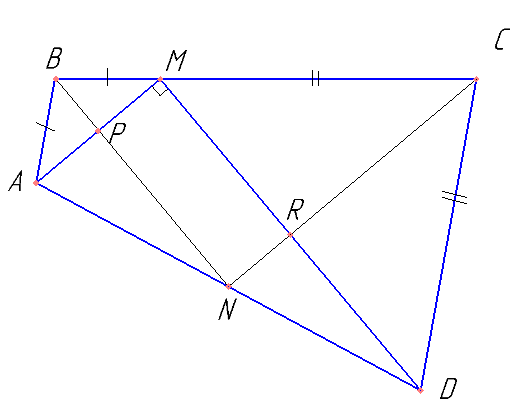
а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD пересекаются на стороне AD.
б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM:MC=1:3, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 18.
Доказать, что срединные перпендикуляры катетов прямоугольного треугольника пересекаются на гипотенузе.
Теорема Фалеса. Как относятся BP к PN, NR к RC?
В выпуклом четырехугольнике ABCD диагонали пересекаются под прямым углом в точке О. АО:ОС=1:3. Площадь треугольника ABD равна 18. Найти площадь треугольника BCD.
В выпуклом четырехугольнике ABCD диагонали пересекаются под прямым углом в точке О. На продолжении стороны BA взяли точку М так, что MD параллельно АС. МА:АВ=1:3. Площадь треугольника ABC равна 21. Найти площадь треугольника ACD.
Ответ: 96.
