Две окружности касаются внутренним образом в точке A, причём меньшая проходит через центр большей. Хорда BC большей окружности касается меньшей в точке P. Хорды AB и AC пересекают меньшую окружность в точках K и M соответственно.
а) Докажите, что прямые KM и BC параллельны.
б) Пусть L — точка пересечения отрезков KM и AP. Найдите AL, если радиус большей окружности равен 10, а BC=16.
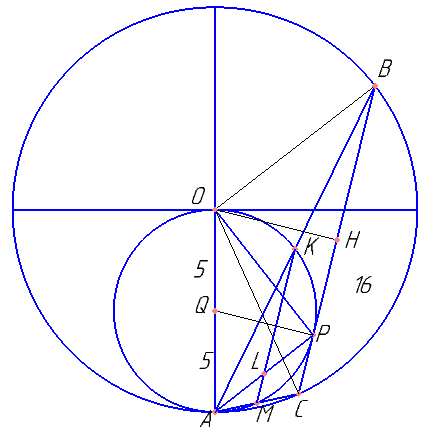
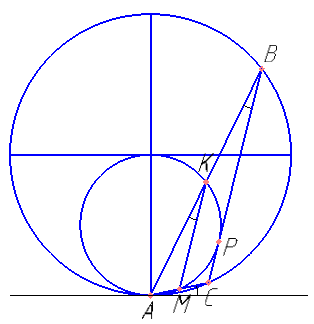
Нужен точный чертеж и линейка с окружностями разных диаметров. Сильно помогают радиусы и высоты.
Надо запомнить эту ситуацию — касание двух окружностей. Постройте касательную в этой точке — найдите равные углы.
Если точно построить, заметно, что KM–средняя линия, что доказывается из равнобедренных треугольников или по равенству вписанного угла и угла между хордой и касательной.
Доказать, что OK перпендикулярно AB, а OL перпендикулярно AC. Убедиться, что треугольники OCA и OBA — равнобедренные.
Доказать, что средняя линия треугольника разбивает пополам любой отрезок соединяющий точку основания и противоположную вершину.
В треугольнике средняя линия и отрезок соединяющий точку основания и вершину пересекаются. Основание разбивается отрезком на две части длиной 4 и 6. На какие части отрезок разбивает среднюю линию?
Вычислить OH, HP из трапеции OHPQ, BP, KL, LM.
Вспомните теорему о пересечении хорд. Вычислить AL.
Решение как в предыдущей задаче не подходит. Выражения из подобия треугольников получаются слишком громоздкими.
Ответ: \( \sqrt{10} \) .
