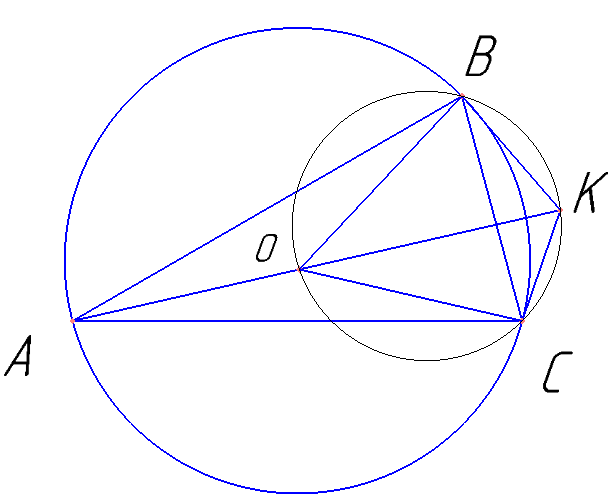
а) Докажите, что четырехугольник ОВКС – вписанный.
б) Найдите радиус окружности, описанной около четырёхугольника OBKC, если cos ∠ВАС =3/5, а ВС=48.
Выполнить дополнительные построения
Как доказать, что 4 точки лежат на одной окружности?
Рассмотрим четырёхугольник ABCD. Для того, чтобы его вершины были расположены на одной окружности, необходимо и достаточно, чтобы выполнялось одно из следующих равенств:
(1) ∠ABD = ∠ACD;
(2) ∠A+ ∠C = 180◦;
(3) KA ·KC = KB ·KD, где K — точка пересечения диагоналей;
(4) MA ·MB = MD ·MC, где M — точка пересечения прямых AB и CD.
Определить тип треугольника AOC.
Если ∠AKC обозначить за x, то ∠BAC= 90◦ — x. Выразить величину угла BOC, OBC.
Найти \( sin(2\alpha) \), если \( cos(\alpha)=0,6 \).
Вспомните теорему синусов.
Ответ: 25.
