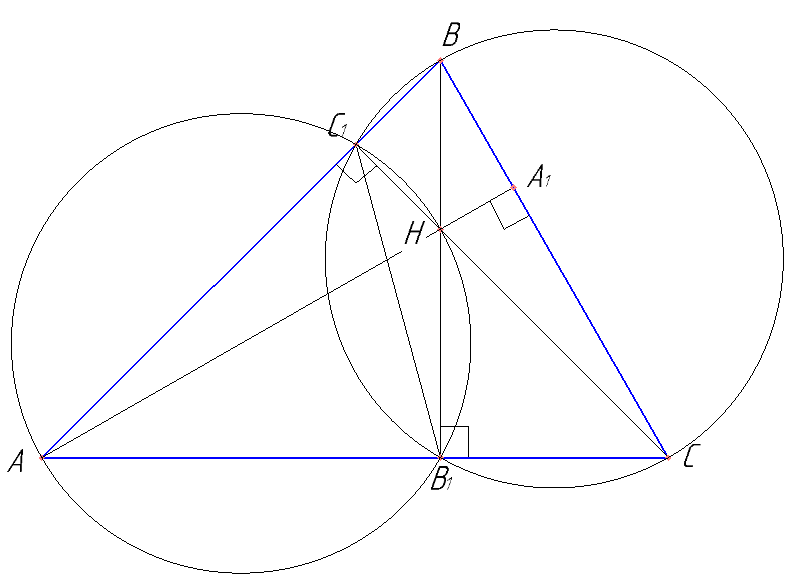
а) Докажите, что ∠AHB1 = ∠ACB.
б) Найдите BC, если AH=8\( \sqrt{3} \) и ∠BAC=60°.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H
а) Докажите, что ∠AHB1=∠ACB.
б) Найдите BC, если AH=10\( \sqrt{3} \) и∠BAC=30°
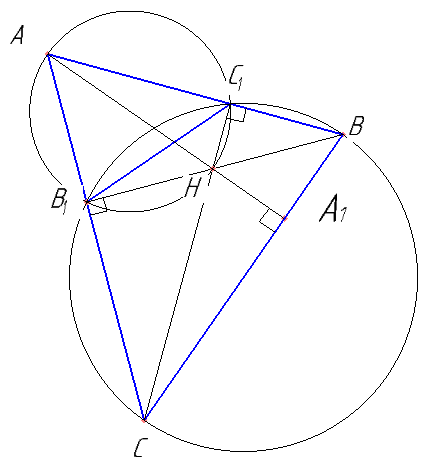
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. Прямая АН пересекает сторону ВС в точке А1. Найти угол АА1В.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке H. Докажите, что ∠BB1C1=∠BCC1.
Найти на чертеже 4 точки лежащие на одной окружности
Во вписанном треугольнике АВС угол А равен 90° Найти отношение диаметра окружности к BC.
Из точки A, лежащей вне окружности проведены две секущие. Одна из них пересекает окружность в точках B и C, а другая в точках D и E. Найти подобные треугольники, вершины которых находятся в перечисленных точках.
Во вписанном треугольнике АВС угол А равен 60°, диаметр окружности — 8\( \sqrt{3} \) Найти BC.
BB1 и CC1 — высоты остроугольного треугольника ABC. Угол А — 60°. Определить коэффициент пропорциональности отрезков АС, АВ отрезкам и АС1 и АВ1.
Ответ: 24; 10.
