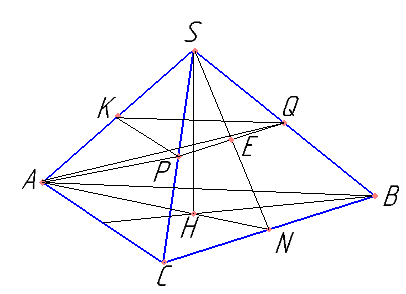
Дана правильная треугольная пирамида SABC, AB=24, высота SH, проведенная к основанию равна 14, точка K середина AS, точка N середина BC. Плоскость, проходящая через точку K и параллельная основанию пирамиды пересекает ребра SB и SC в точка P и Q соответственно.
а) Докажите, что PQ проходит через середину SN.
б) Найдите угол между плоскостью основания и плоскостью APQ.
Докажите, что PQ средняя линия треугольника BSC.
Доказать, что высота в равнобедренном треугольнике проведенная к основанию и средняя линия, параллельная основанию точкой пересечения делятся пополам.
Обоснуйте, что искомый угол EAN.
Найти AN, NE, медиану AE.
Используя теорему косинусов, найти косинус угла EAN.
Ответ; \( arccos(\frac{10\sqrt{1047}}{349}) \)