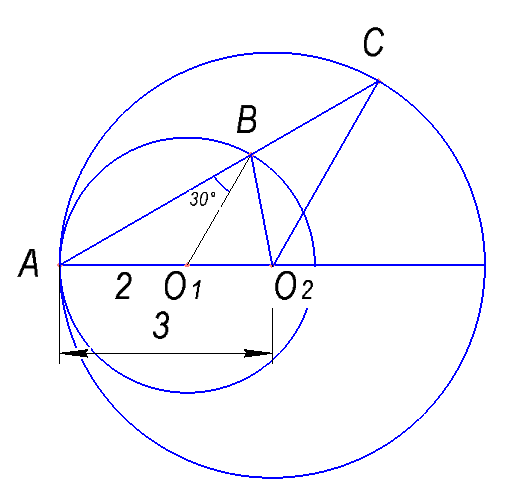
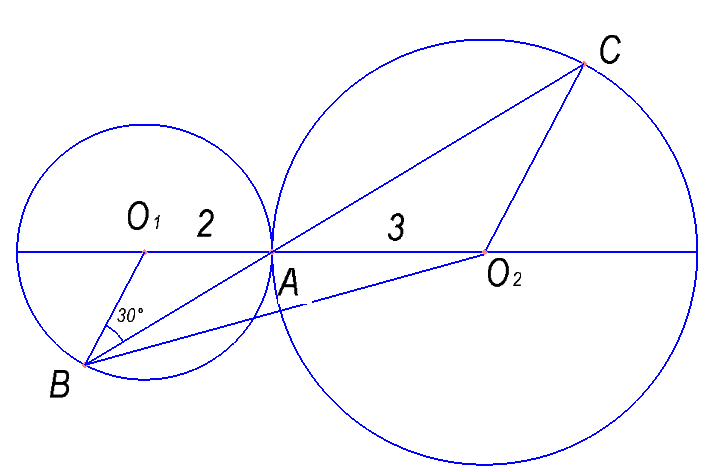
Окружности радиусов 5 и 8 с центрами O1 и O2 соответственно касаются в точке A. Прямая, проходящая через точку A, вторично пересекает меньшую окружность в точке B, а большую — в точке C. Найдите площадь треугольника BCO2, если угол ABO1 равен 15°.
В прямоугольном треугольнике ABC с катетами AC=5 и BC= 6. На катете AC взяли точку K, так, что CK=2, а на катете BC взяли точку M, так, что CM=4. Найти площадь четырехугольника ABMK.
В равнобедренном треугольнике AOC боковые стороны AO и CO равны 3, угол при основании равен 30°. Найти площадь треугольника.
В равнобедренном треугольнике ABO боковые стороны AO и BO равны 2, а угол A равен 30°. На продолжении стороны AO за точку O отложили отрезок OK=1. Найти площадь треугольника KBA.
Ответ: 0,75\( \sqrt{3} \) или 3,75\( \sqrt{3} \); 6 или 26.
