В параллелограмме ABCD угол A острый. На продолжениях сторон AD и CD за точку D выбраны точки N и M соответственно, причем AM=AD и CN=CD.
а) Докажите, что BM=BN.
б) Найдите MN, если AC=7,\( sin BAD=\frac{7}{25} \).
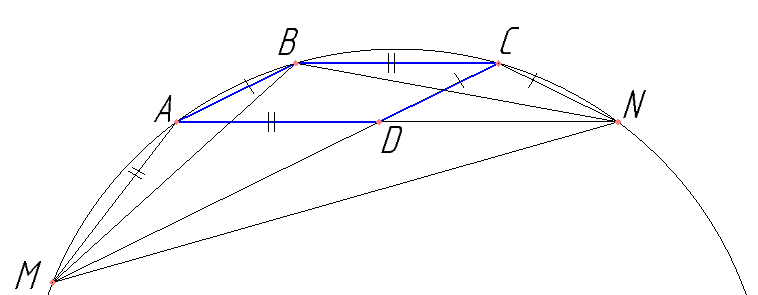
Определить тип четырехугольников ABCN и MABC.
Доказать, что точки M, A, B, C, N лежат на одной окружности.
Если хорды окружности равны, то соответствующие дуги равны, а наоборот?
Есть ли на чертеже угол опирающийся на ту же дугу, что и угол BAD?
Диагонали в равнобедренной трапеции равны?
В равнобедренном треугольнике боковая сторона равна 7, а синус угла при основании равен \( \frac{7}{25} \). Найти основание.
Ответ: 13,44.
