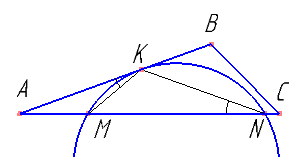
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 32 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если \( cos\angle BAC=\frac{2\sqrt{2}}{3} \).
Найти AK, используя теорему о хорде и касательной.
Найти KM, используя теорему косинусов.
В треугольнике AKN \( cos\angle KNA=\frac{2\sqrt{2}}{3} \). Найти \( sin \angle KNA \).
Во вписанном треугольнике сторона равна 9, а синус противолежащего угла \( \frac {1}{3} \). Найти радиус окружности.
Ответ: 13,5