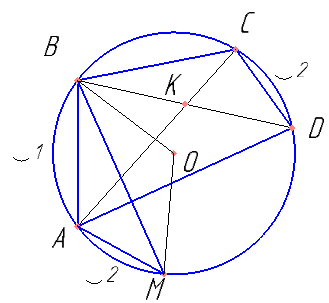
Четырёхугольник ABCD со сторонами AB=25 и CD=16 вписан
в окружность. Диагонали AC и BD пересекаются в точке K,
причём ∠AKB=60º. Найдите радиус окружности, описанной около этого четырёхугольника.
Найти чему равна градусная мера суммы дуг \( \smile AB \) и \( \smile CD \).
Построить хорду AM=CD. Найти градусную меру дуги \( \smile BCM \). Найти величину угла \( \angle BAM \).
Найти BM. Найти радиус окружности в которую вписан треугольник со стороной \( \sqrt{1281} \) и противолежащим углом 120º
Знание теоремы синусов, косинусов, теоремы об угле между пересекающимися хордами обязательно.
Ответ: \( \sqrt{427} \)