В правильной треугольной призме ABCA1B1C1 сторона AB основания равна 8, а боковое ребро AA1 равно 7. На ребре CC1 отмечена точка M, причем CM=1.
а) Точки O и O1 центры окружностей, описанных около треугольников ABC и A1B1C1 соответственно. Докажите, что прямая OO1 содержит точку пересечения медиан треугольника ABM.
б) Найдите расстояние от точки A1 до плоскости ABM.
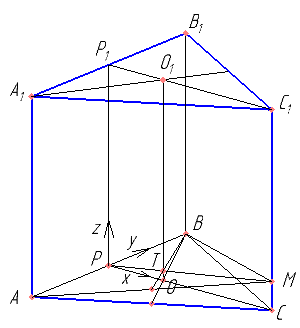
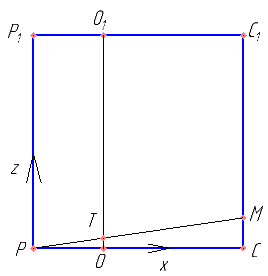
Введем систему координат. Определить координаты точек P, B, C, O, M, T, O1, A1. Найти координаты векторов \( \vec{OO_1} \), \( \vec{OT} \). Доказать, что эти векторы коллинеарны.
Найти координаты вектора \( \vec {PM} \). Составим вектор \( \vec n (-1,0, 4\sqrt{3}) \), перпендикулярный вектору \( \vec {PM} \). Обосновать, что вектор \( \vec n \)перпендикулярен плоскости ABM. Составить уравнение плоскости ABM перпендикулярной вектору \( \vec n \) и проходящей через точку P.
Найти расстояние от точки A1(0, -4, 7) до плоскости заданной формулой \( -x+4\sqrt{3}z=0 \).
Ответ: \( 4\sqrt{3} \)
