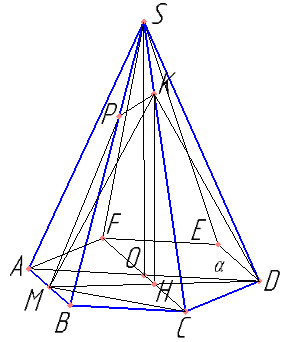
В правильной шестиугольной пирамиде SABCDEF сторона основания AB=2 , боковое ребро SB=5. Точка M середина ребра AB. Через точки M и D перпендикулярно плоскости ABC проведена плоскость α. Прямая SC пересекает плоскость α в точке K.
а) Докажите, что MK=KD.
б) Найдите объем пирамида MKCD.
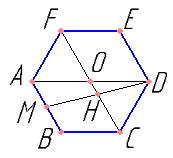
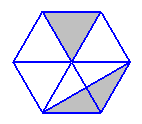
Хорошо помогает понимание того, что правильный шестиугольник состоит из 6 равносторонних треугольников и площади закрашенных треугольников одинаковы. А также, знание того, что медиана делит треугольник на два равных по площади.
Построение сечения: MD, HK || OS — нашли на чертеже точку K. Аналогично для точки P.
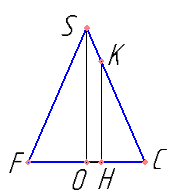
Т.к. OC || AB, то OH — средняя линия треугольника ADM. Следовательно MH=HD. Следовательно — треугольники MHK и DHK равны.
Объемы пирамид MKCD и KMCD равны. Высота KH считается из подобия треугольников CSO и CKH. \( S_{MDC}=1,5S_{AOB} \)
Ответ: \( \frac{9\sqrt{7}}{8} \)
