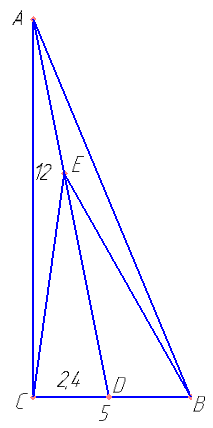
На прямой, содержащей биссектрису AD прямоугольного треугольника ABC с прямым углом C, взята точка E, удалённая от вершины A на расстояние, равное \( \sqrt {26} \). Найдите площадь треугольника BCE, если BC=5, AC=12.
Как известно, площадь треугольника можно вычислить по формуле:
\[ S=\frac{1}{2}ab* sin C \]
Если сторона а треугольника увеличится на 2, а сторона b и угол C останутся прежними, как измениться площадь треугольника?
Теорема Пифагора. Найти AB.
Теорема о биссектрисе треугольника. Найти AD.
Найти площадь треугольников ACD, ADB.
Найти биссектрису AD. Вынести из под корня \( \sqrt{149,76} \).
В треугольнике с основанием \( 2,4\sqrt{26} \) и площадью 30, основание увеличили на \( \sqrt{26} \). Найти площадь получившегося треугольника.
Ответ: 17,5 или 42,5.