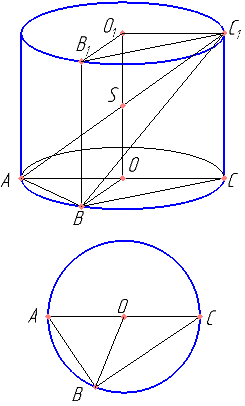
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A и B, а на окружности другого основания — точки B1 и C1, причём BB1 — образующая цилиндра, а отрезок AC1 пересекает ось цилиндра.
а) Докажите, что угол ABC1 прямой.
б) Найдите угол между прямыми BB1 и AC1, если AB=6, BB1=15, B1C1=8.
Построим CC1 || OO1. Следовательно CC1 перпендикулярна плоскости основания — образующая. AC содержит центр основания — диаметр. Следовательно ABC — прямоугольный треугольник.
Определить взаимное расположение BA, BB1, BC. AB перпендикулярна любой прямой лежащей в плоскости B1BC?
Обоснуйте, что точка S делит OO1 пополам.
Обоснуйте, что ∠O1SC1 — искомый угол. Найти AC, OS, \( tg(\angle O_1SC_1) \)
Ответ:\( arctg(\frac{2}{3}) \)