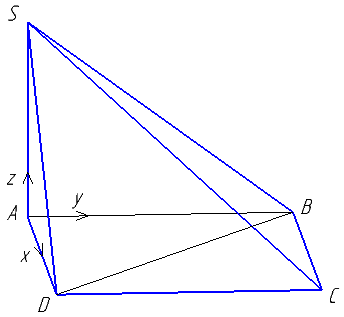
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=6. Длины боковых рёбер пирамиды SA=\( \sqrt{21} \), SB=\( \sqrt{85} \), SD=\( \sqrt{57} \).
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=4 и BC=3. Длины боковых рёбер пирамиды: SA=\( \sqrt{11} \), SB=\( \sqrt{33} \), SD=\( \sqrt{25} \).
а) Докажите, что ребро SA — высота пирамиды.
б) Найдите угол между прямой SC и плоскостью ASB.
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=8 и BC=15. Длины боковых рёбер пирамиды SA=\( \sqrt{111} \), SB=\( 5\sqrt{7} \), SD=\( 4\sqrt{21} \).
а) Докажите, что SA — высота пирамиды.
б) Найдите угол между прямыми SC и BD.
Доказать, что треугольник со сторонами 6, \( \sqrt{21} \),\( \sqrt{57} \) прямоугольный.
Найти координаты векторов SC и BD. Найти угол между ними.
Прямая a пересекает плоскость α. Прямая n перпендикулярна плоскости α. Угол между прямыми a и n равен 15°. Найти угол между прямой a и плоскостью α.
Косинус угола между плоскостью и прямой может быть отрицательным?
Ответ: \( arccos(\frac{14}{55}) \), \( \frac{\pi}{2}-arccos(\frac{6}{11}) \), \( arccos(\frac{161}{340}) \)