В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 18, а боковые рёбра равны 15. Точка R принадлежит ребру MB, причём MR:RB=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки C и R параллельно прямой BD.
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 12, а боковые рёбра равны 24. Точка G принадлежит ребру MA, причём MG:GA=2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки B и G параллельно прямой AC.
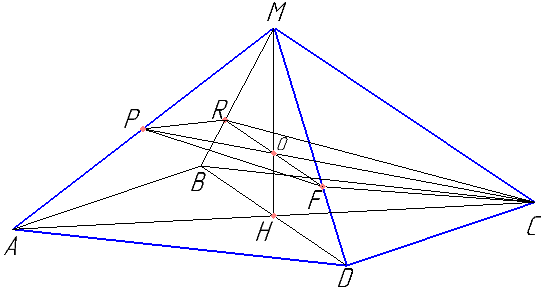
Обоснуйте параллельность BD и RF, перпендикулярность RF и PC.
Найти отношение MO к OH. Найти RF.
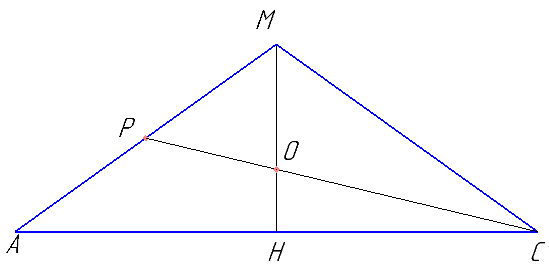
Обосновать, что O — точка пересечения медиан. Найти медиану PC.
Воспользоваться универсальной формулой расчета площади выпуклого четырехугольника.
Ответ:\( 117\sqrt{2} \), 96.
